Simone达布中值定理
的有关信息介绍如下：达布中值定理：
设y=f(x)在(A,B)区间中可导，且[a,b]包含于(A,B)，f'(a)<f'(b)，则对于任意给定的η：f'(a)<η<f'(b)，都存在一点c∈(a,b)，使得f'(c)=η。
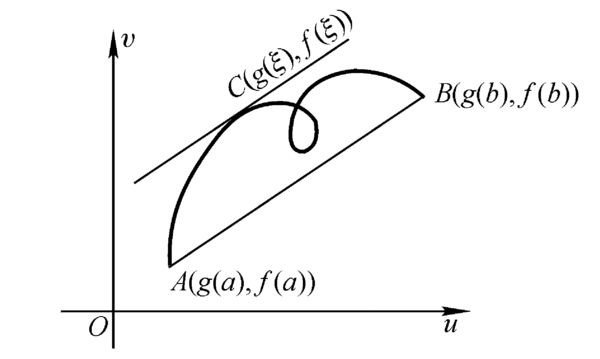
数学表达形式：
设y=f(x)在(A,B)区间中可导，且[a,b]包含于(A,B)，f'(a)<f'(b)，则对于任意给定的η：f'(a)<η<f'(b)，都存在一点c∈(a,b)，使得f'(c)=η。
等价形式：
设f(x)在 [a,b]上可微，若在 [a,b]上f′(x)不等于0，则f′(x)在[a,b] 上保持定号(恒正或恒负)。
其它表达形式：
若函数f(x)在[a,b]上可导，则f′(x)在[a,b]上可取f′(a)和f′(b)之间任何值。
